1.1 出力和位移的关系
位移△L0:是压电陶瓷产生的位移,这个数值是在空载条件下测得,即在压电陶瓷产生位移过程中不受任何阻力。对陶瓷施加电压后,测得相应位移。
出力Fmax:是压电陶瓷产生的最大出力,这个数值是压电陶瓷在位移为0时,测得的出力,即抵抗大刚度负载的推力。
kA=Fmax/△L0
假设把陶瓷固定在两面墙之间,施加最大电压给压电陶瓷,由于两面墙的刚度很大,压电陶瓷无法伸长,位移为零,这时的出力为最大出力。但是事实上,任何物体都会表现出一定的弹性模量,这里我们把墙的弹性忽略不计。
当外部机械结构的刚度为零时,给压电陶瓷加最大电压,压电陶瓷产生最大位移。这时出力为零。出力与位移的关系如下图所示。

只要外部连接机械结构存在刚度,则陶瓷的位移就一定会有损失,位移损失的大小取决于外部机械结构的刚度,外部机械结构刚度越大,损失的位移也就越大,当外部机械结构的刚度与陶瓷的刚度相同时,位移与出力为最大位移与出力一半,陶瓷能效得到最大的利用。
如果想用压电陶瓷产生位移,那么这个陶瓷一定是极化过的。该材料的大部分偶极子必须在一个方向上。如果在偶极子的方向(这里z方向)施加电场,陶瓷致动器将沿电场方向伸长(纵向效应),垂直电场方向收缩(横向效应)。
位移是由下式表示:
纵向效应
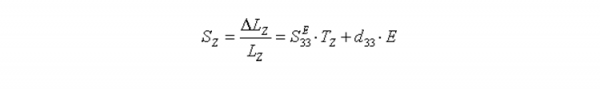
(1.0.1)
横向效应

(1.0.2)
S--应变,相对位移;
T = F / A--机械的弹性压力;
Sii--弹性系数;
ΔLZ--驱动器在Z向的位移;
LZ--压电致动器有效部分的长度;
E=kA/ds--外部预加载弹簧的刚度系数;
kA--压电陶瓷的刚度的刚度。
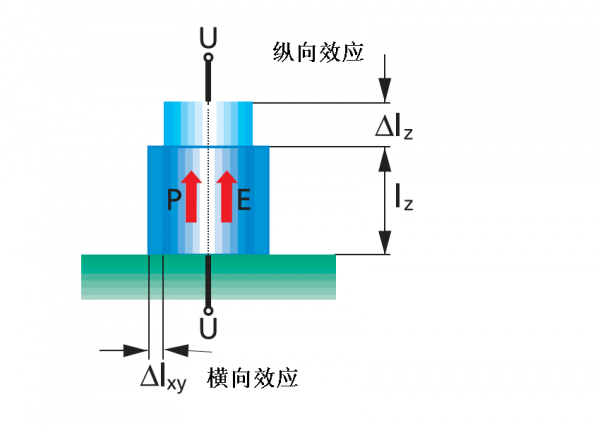
图 1.1 压电陶瓷的纵向效应和横向效应
如果没有特别提出,我们说的压电效应都是指纵向效应。但是对于横向效应,所有的关系可以以相同的方式表述。

(1.0.3)
公式(1.0.3)的第一项把陶瓷致动器作为刚度为CT的弹簧的的机械特性。第二项描述的是在电场E下的伸长位移。
1.2 没有电压施加到致动器,E = 0
陶瓷致动器被短路,公式(1.0.3)变为S =ΔL/ L0= S33·T。致动器的变形量由其刚度CET决定,因为额外负载力的作用,致动器会被压缩而变短。
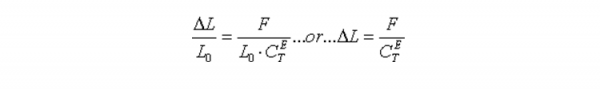
(1.1.1)
L0--致动器的长度
1.3 无外力,F=0
叠堆陶瓷在没有任何预载力和外力的情况下,位移如下式:
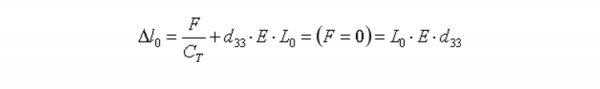
(1.2.1)
最大位移取决于叠堆陶瓷的长度、叠堆陶瓷材料和场强。
例 让我们考虑一个这样参数的叠堆陶瓷:
压电常数d33=635×10-12m/ V;叠堆长度L0=16mm;单片的厚度为100μm。工作电压是150V。电场强度为E=1.5kV/mm。在无外力的情况下,根据公式1.2.1,我们可以很容易的得出陶瓷的位移ΔL0=15μm。




